Main Thoughts
- First analyses the workflow log transition probabilities between activities to build the Markov transition matrix;
- Then mines the process logic relationship by defining a set of rules of logical relational
- At last design the process mining algorithm to establish the actual structure relationship between the activities in order to reconstruct the workflow.
Methods to find incomplete logs
- List the set of the end events of the log, if an instance’s log end event does not belong to the set
- If a task only has the start event without a corresponding end event
Symbol Description
| symbol | meaning | symbol | meaning |
|---|---|---|---|
| n | execution times of workflow | $X = \{x_0,x_1…x_k\}$ | set of activities |
| P | workflow transition matrix | $X_s$ | start process |
| $X_E$ | end process | > | sequence relationship |
| $\rightarrow$ | casual relationship | # | selection relationship |
| // | synchronous relationship | $\diamond$ | circle relationship |
Build Markov Transition Matrix
- $p_{ij} = m_{ij}/n$, $m_{ij}$ means the one step transition times from activity $x_i$ to $x_j$ in the n workflow instances
Logic Relationship Mining Rules
(1) Start of the process: $\exists x_j \in X$, and $\forall x_i~\in~X$, if $p_{ij} = 0$, then $X_s = x_j$
(2) End of the process: $\exists x_i \in X$, and $\forall x_j \in X$, if $p_{ij} = 0$, then $X_E = xi$
(3) Sequence relationship: $\forall x_i,~x_j \in X$, if $p_{ij} \neq 0$, then $x_i >x_j$
(4) Casual relationship: $\forall x_i,~x_j \in X$, if $p_{ij} = 1$, then$x_i \rightarrow x_j$
(5) Synchronous relationship:
- And-Split: if $p_{i \eta_1} = p_{i\eta_2} = … = p_{i\eta_k}= \frac{1}{k}\neq 0$, and $x_i \neq x_{\eta_k}$, then $\{x_{\eta_1}//x_{\eta_2}//..//x_{\eta_k},x_i > x_{\eta_k}\}$, $x_i$ is the And-Split activity node
- And-Join: if $p_{\eta_1 i} = p_{\eta_2 i}= …=p_{\eta_k} = \frac{1}{k} \neq 0$, and $x_i \neq x_{\eta_k}$, then $\{x_{\eta_1}//x_{\eta_2}//..//x_{\eta_k}, x_{\eta_k}>x_i \}$, $x_i$ is the And-Join activity node
(6) Selection relationship:
- OR-Split: $\exists x_i, x_{\eta_k} \in X, p_{i\eta_k} >0$, if $\sum_k p_{ij} = 1$, then $\{x_{\eta_1}$# $x_{\eta_2}$# ..# $x_{\eta_k},x_i > x_{\eta_k}\}$, $x_i$ is the OR-Split activity node
- OR-Join: $\exists x_i, x_{\eta_k} \in X, p_{i\eta_k} >0$, if $\sum_k p_{\eta_ki} = 1$, then $\{x_{\eta_1}$#$x_{\eta_2}$#..#$x_{\eta_k},x_{\eta_k} > x_i\}$, $x_i$ is the OR-Join activity node
(7) Self-circulation relationship: $\exists x_i \in X, x_{\eta_k} \ in X - \{x_i\}$, if $p_{ii} = p(p \neq 1)$, then $\{\diamond x_i; x_i > x_{\eta_k}\}$
(8) Multi-step cycle relationship:
- $\forall x_i, x_{\eta_k} \in X, x_i \neq X_S, x_i \neq X_E, X_{re} \neq \emptyset$, if $p_{ij} = 0, p_{ji} > 0~and~\exists k(k\leq n-1)$, which makes $p_{ij}^{(k)} > 0 (p_{ij}^{(k)}\in p^k)$, then there is a multi cycle between $x_i$ and $x_j$, and $x_j > x_i$; $X_{re}$ = $X_{re} +\{x_i,x_j\}$; and do Refunction().
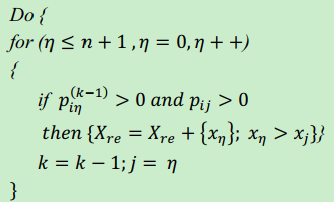
While ($k \geq 2$) the activities in $X_{re}$ has cycle relationship, i.e. $x_j \diamond x_i \diamond x_{\eta_1} \diamond …\diamond x_{\eta_{k-3}}$
The start $X_{rS}$ and end $X_{rE}$ of the multi-step cycle:
If $\exists x_{\eta_k}\in X_{re}, x_i \in X-X_{re}$, and $p_{i\eta_k} > 0 $, then $\{X_{rS} = X_{\eta_k};x_i > X_{rS}\}$
If $\exists x_{\eta_k}\in X_{re}, x_i \in X-X_{re}$, and $p_{\eta_k i} > 0 $, then $\{X_{rE} = X_{\eta_k};X_{rE}>x_i \}$
Design of Process Mining Algorithm Based on the Rules
- INPUT: Markov matrix P, activities set X
- OUTPUT: $W_{and} = \{(x_{\eta_i},x_{\eta_2},…)|x_{\eta_1}//x_{\eta_2}//…\}$, $W = \{(x_i,x_j)|x_i\rightarrow x_j~or~x_i >x_j~or~ x_i \diamond x_j\}$,$W_{select} = \{(x_{\eta_i},x_{\eta_2},…)|$$x_{\eta_1}$#$x_{\eta_2}$#$ …\}$
