模型评估与选择

本章基本概念

错误率(error rate): 在m个样本中假设有a个样本分类错误，则错误率$E = a/m$,相应地，$1-a/m$称为精度(accuracy)
实际预测输出与样本真实输出的误差称为“误差”(error),在训练集上的误差称为训练(training)误差\经验(empirical)误差，在新样本上的误差称为泛化误差
过拟合overfitting：泛化能力很差；欠拟合(underfitting):对训练样本的一般性质尚未学习好。

评估方法

注意测试集和训练集的数据分布应该尽量保持一致，一般采用分层采样(stratified sampling)

留出法

将数据集D拆分为两个互斥的集合，其中一个集合为训练集S，另一个为测试集T，$D = S\cup T,S\cap T =\emptyset$
一般采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果

交叉验证法/K折交叉验证

将数据集划分为k个大小相似的互斥子集，即$D = D_1\cup D_2\cup … \cup D_k,D_i\cap D_j =\emptyset(i\neq j)$,注意每个子集$D_i$都尽可能保持数据分布的一致性
与留出法相似，通常要随机使用不同划分重复p次，最终的结果是这p次k折交叉验证结果的均值。

自助法

对于样本集D，采用有放回采样：每次随机取一个，然后放回，直到构成一个新的样本集$D’$,样本在m次采样中始终不被采集到的概率为$(1-\frac{1}{m})^m = \frac{1}{e}\approx 0.368$,故而约有36.8%的样本未出现在D’中，用$D/D’$用作测试集

总结

自助法在数据集较小，难以有效划分训练/测试集时很有用，而且能够从初始集中产生多个不同的训练集，对于集成学习等方法有很大的好处；但是他改变了初始数据集的分布，会引入估计偏差(estimation error)，因此在数据量组都的情况下，推荐使用留出法和交叉验证法。

性能度量

回归任务

回归任务最常用的性能度量就是“均方误差(mean squared error)” $E(f;D)=\frac{1}{m}\sum^m_{i=1}(f(x_i)-y_i)^2$ 更一般地，对于数据分布D和概率密度函数p(.),均方误差可描述为 $E(f;D) = \int_{x\sim D}(f(x)-y)^2p(x)dx$

分类任务

对于样例集D，

错误率定义为
$E(f;D)=\frac{1}{m}\sum^m_{i=1}\|(f(x_i)\neq y_i)$
精度定义为
$acc(f;D) = \frac{1}{m}\sum^m_{i=1}\|(f(x_i) = y_i)$
更一般地，对于数据分布D和概率密度函数p(.)，错误率和精度可分别描述为
$E(f;D)=\int_{x\sim D}\|(f(x)\neq y)p(x)dx\\ acc(f;D) = \int_{x\sim D}\|(f(x) = y)p(x)dx = 1-E(f;D)$

混淆矩阵(confusion matrix):

真实情况	预测结果	预测结果
	正例	反例
正例	TP(真正例)	FN(假反例)
反例	FP(假正例)	TN(真反例)

查准率P: $P = \frac{TP}{TP+FP}$

查全率R：$R = \frac{TP}{TP+FN}$

查准率和查全率是相互矛盾的量，从而有P-R曲线，若一个学习器的P-R曲线被另一个学习器的曲线完全包住，则可断言后者的性能优于前者；对于互相交叉的，可以看平衡点，即查准率等于查全率的点，哪个比较大就认为哪个就好一点

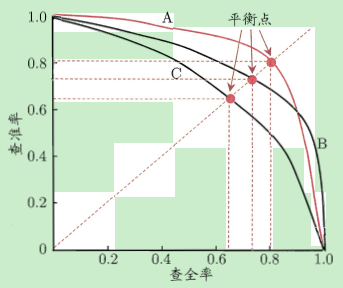
在一些应用中，查准率和查全率的重视程度不同，可用F1度量来进行评价：

$F_{\beta} = \frac{(1+\beta^2)\times P\times R}{(\beta^2\times P)+R}$

如果是在n个二分类混淆矩阵上综合考察查准率和查全率，有两种方法

在各混淆矩阵上分别计算出查准率和查全率，再计算平均自，得到宏查准率，宏查全率以及相应的宏F1
现将各混淆矩阵的对应元素进行平均，得到TP,FP,TN,FN的平均值，而后计算出微查准率，微查全率和微F1

ROC 与 AUC

ROC(受试者工作特征)，横纵坐标分别为：

假正例率：$FPR = \frac{FP}{TN+FP}$

真正例率：$TPR = \frac{TP}{TP+FN}$
- 若一个学习器的ROC曲线被另一个学习器的曲线完全包住，则可断言后者的性能优于前者；如果交叉，则一般用AUC(ROC曲线下的面积)来衡量 $AUC = \frac{1}{2}\sum^{m-1}_{i=1}(x_{i+1}-x_i).(y_i+y_{i+1})$ 给定$m^+$个正实例和$m^-$个反例，令$D^+$和$D^-$分别表示正反例集合，则排序损失(loss)定义为： $l_{rank} = \frac{1}{m^+m^-}\sum_{x^+\in D^+}\sum_{x^-\in D^-}(\|(f(x^+)<f(x^-))+\frac{1}{2}\|(f(x^+)=f(x^-)))$ 即，若正例的预测值小于反例，则记一个罚分，若相等，则记0.5个罚分 $AUC = 1-L_{rank}$
代价敏感错误率与代价曲线

不同的错误造成的代价可能是不同的，此时要赋予其权重。

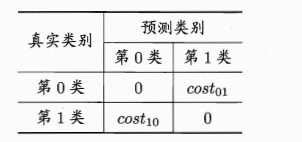
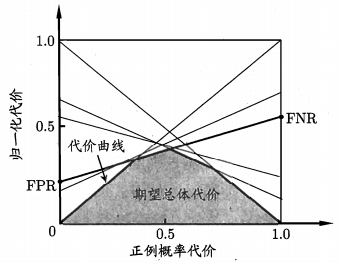
一般$cost_{ii} = 0$,若将第0类别判别为比第1类所造成的损失更大，则$cost_{01}>cost_{10}$,损失程度相差越大，两个代价矩阵的差值越大。此时对应的代价敏感错误率为

相应的，此时ROC曲线不能直接反应出学习期的期望总体代价，而可以通过代价曲线（cost curve）来达到该目的：
- 横轴为取值为[0,1]的正例概率代价：
  $P(+)cost = \frac{p\times cost_{01}}{p\times cost_{01}+(1-p)\times cost_{10}}$
  其中p为样例为正例的概率
- 纵轴为取值为[0,1]的归一化代价
  $cost_{norm} = \frac{FNR\times p\times cost_{01}+FPR\times(1-p)\times cost_{10}}{p\times cost_{01}+(1-p)\times cost_{10}}$
  $FNR = 1-TPR$是假反例率，ROC曲线上的没一点对应了代价平面上的一条线段。

比较检验

此部分内容见整理的数理统计内容