神经了的ODE: Neural CDE

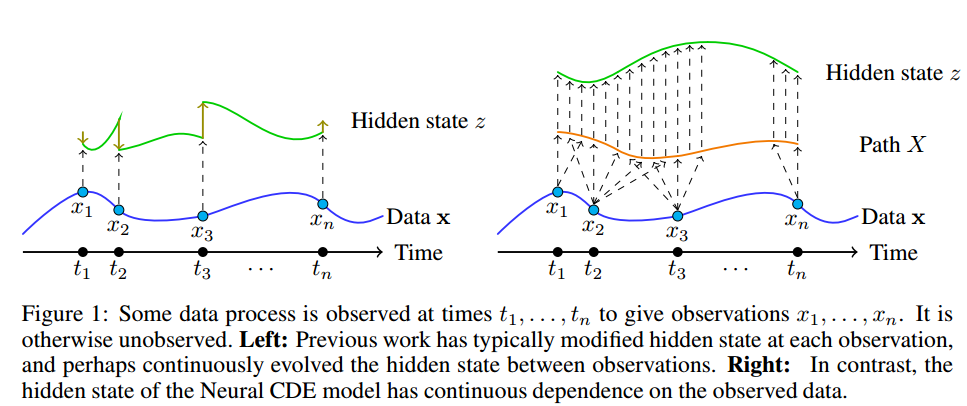
Neural Controlled Differential Equations for Irregular Time Series

Neural ODE的缺点是一旦初值确定，轨迹便确定，中间无法对轨迹进行修正，本文引入受控微分方程概念，使得后续拿到的数据得到进一步利用。ArXiv, code.

• 假设$\tau, T\in R$, 且$\tau <T$, $v,\omega$为正整数， $X:[\tau, T]\rightarrow R^v$为一个有界连续函数(即X是满足Lipschitz性质的)。$f:R^\omega \rightarrow R^{\omega\times v}$是连续映射函数，$\zeta\in R^\omega$, 且有连续映射 $z:[\tau, T]\rightarrow R^{\omega\times v}$, 并定义

  $$z_t = z_\tau + \int^t_{\tau} f(z_s)dX_s~~~\text{for}~~t\in (\tau, T]$$

  其中 $X_s\in R^v, f(Z_s)\in R^{\omega \times v}$, 上式被称作 $\text{Controlled differential equation}$.

• 与一般基于ODE的时序预测方法不同，本文在考虑后续状态的同时，可以保证隐藏状态z是连续变化的。

• 对(1)式进行扩展，可以得到$\text{Neural Controlled Differenrial Equations}$的定义为：

  $$z_t = z_{t_0} + \int^t_{t_0} f_{\theta}(z_s)dX_s~~~\text{for}~~t\in (t_0, t_n]$$

  其中$z_{t_0} = \zeta_{\theta}(x_0, t_0)$

  • 本文中$X:[\tau, T]\rightarrow R^v$是通过自然边界下三次样条插值法来确定的
  • $f_{\theta}:R^\omega \rightarrow R^{\omega\times (v+1)}$表示任意神经网络，$w$是超参数，表示隐藏状态的维度
  • $\zeta_{\theta}: R^{v+1}\rightarrow R^{\omega}$表示任意依赖于参数$\theta$的神经网络

• 本文将 $\text{Controlled differential equation}$转化为普通的ODE方程，从而能够通过$\text{Neural ODE}$中的方法进行求解，假设

  $$g_{\theta, X}(z,s) = f_{\theta}\frac{dX}{ds}(s)$$

  则很容易得到

  $$\begin{equation} \begin{aligned} z_t &= z_{t_0} + \int^t_{t_0} f_{\theta}(z_s)dX_s \\ &= z_{t_0} + \int^t_{t_0}f_{\theta}(z_s)\frac{dX}{ds}(s)ds\\ &= z_{t_0} + \int^t_{t_0} g_{\theta,X}(z_s, s)ds. \end{aligned} \end{equation}$$